Timed Device is a library for Arduino / ESP 8266/32 embedded platforms written to emulate a simple plug in timer for an electrical device, where pins in a ring are set to define hour/minute status. Designed to be simple and lightweight optimisation is for low memory.

Arduino ATMega328 and related embedded microcontrollers provide internal high precision clock based timers suitable for events with second, millisecond and fine granularity (to clock speed 8 / 16 mhz).
When lower precision is sufficient, recurring timers for example where an event should occur on a specific minute, hour or day of week, a lightweight implementation can be achieved and storage for internal data structures can be optimised, a significant win factor on embedded systems where memory use is constrained.
The library follows an object orientated design pattern resulting in an extensible, scale-able architecture suitable for controlling from one to a large number of devices sharing a common timing core with each timed device class able to implement specific instructions for switching on/off.
Example use cases:
- Switch lights or any electrical relay device on/off
- Activate a pump or valve
- Open/Close blinds, curtains or shutters
- Control a fan, heat source or air conditioning
How to Define Time
In C time.h the tm structure has the following definition −
struct tm {
int tm_sec; /* seconds, range 0 to 59 */
int tm_min; /* minutes, range 0 to 59 */
int tm_hour; /* hours, range 0 to 23 */
int tm_mday; /* day of the month, range 1 to 31 */
int tm_mon; /* month, range 0 to 11 */
int tm_year; /* The number of years since 1900 */
int tm_wday; /* day of the week, range 0 to 6 */
int tm_yday; /* day in the year, range 0 to 365 */
int tm_isdst; /* daylight saving time */
};
While this structure is useful for point in time defined events, in case of a recurring timers this can be simplified.
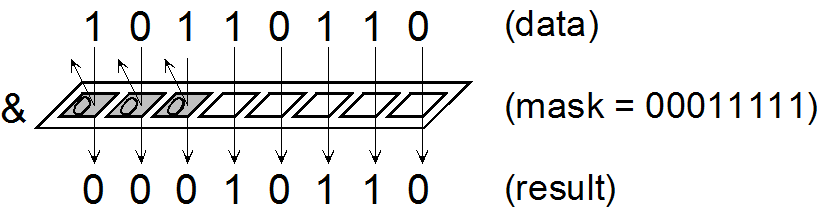
If hour precision is sufficient, a single 32 bit mask can be used:
// Bitmask defines hours (from 24h hours) device is on (1) or off (0) // 0b 00000000 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 long hourTimerBitmask =0b00000000001111111111111111100000;
Day of week (bit index 0 = Sunday – 6 Saturday) can be defined similarly:
long dayOfWeekTimerBitmask = 0b0101010;
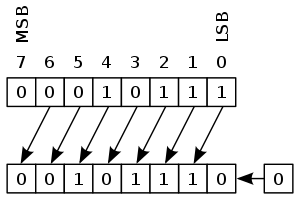
With bitmasks we can determine if an event is scheduled using bit shifts:
// Check if bit at pos n is set in 32bit long l
bool Timer::_checkBitSet(int n, long * l)
{
bool b = (*l >> (long) n) & 1U;
return b;
}
To check if an hour timer bitmask is on/off for 7am:
bool isSet = _checkBitSet(7, hourTimerBitmask)
For a more detailed guide to Bitmasks, shifts and bitwise operations see this article.
An on / off time occuring at specific (hour:minute) intervals can be defined as:
typedef struct tmElements_t {
uint8_t Min;
uint8_t Hour;
};
We can use a struct as container for an array of 1..n pairs of on/off times occurring on specified weekdays:
#define SZ_TIME_ELEMENT 2
typedef struct tmElementArray_t {
unsigned long Wday; // bitmap - days of week (bit index 0 = Sun - 6 Sat)
struct tmElements_t onTime[SZ_TIME_ELEMENT];
struct tmElements_t offTime[SZ_TIME_ELEMENT];
};
With these data structures we can setup up a pair of on/off times (08:00 -> 08:10 and 19:00 -> 19:30) to occur on Sun, Mon, Thur, Fri:
// create variables to define on/off time pairs struct tmElements_t t1_on, t1_off, t2_on, t2_off, t3_on, t3_off; struct tmElementArray_t timeArray; t1_on.Hour = 8; t1_on.Min = 0; t1_off.Hour = 8; t1_off.Min = 10; t2_on.Hour = 19; t2_on.Min = 0; t2_off.Hour = 19; t2_off.Min = 30; timeArray.n = 2; // number of time pairs timeArray.Wday = 0b00110011; // define days of week timer is active on timeArray.onTime[0] = t1_on; timeArray.offTime[0] = t1_off;
Check if a recurring timer is set
How we check a timer (whether bitmask or time based) depends on the type of time source we have.
Most familiar time source on Arduino is millis() function providing elapsed time in milliseconds since device reset / startup.
This is useful for timing events in a non-blocking way at recurring intervals:
if (millis() >= sampleTimer + sampleInterval)
{
... do something
sampleTimer = millis();
}
But what if we want to schedule in terms of hour, minute or day of week based on current time?
To achieve this a micrcontroller is combined with a Real Time Clock module, providing a battery backed time source that once synced (for example to an NTP time source) maintains current time even when device is switched off.

Arduino DS1307/3231 RTC modules have supporting libraries (for example RTCLib from Adafruit) to obtain current time usually in form of:
DateTime now = rtc.now();
Where DateTime object provides an API to return specific time elements:
Serial.print(now.hour());
Serial.print(':');
Serial.println(now.minute());
Serial.print(now.dayOfTheWeek());
Is an event scheduled (at a specific point in time)?
In C function overloading can be used to provide multiple interfaces to an isScheduled() method according to timer precision / time source type :
bool isScheduled(int h); bool isScheduled(int h, int d); bool isScheduled(int m, int h, int d); bool isScheduled(unsigned long ts); (Where h = hour, m = minute, d = week day)
Most users of Unix based systems are familiar with “timestamp” a 32bit unsigned long representing elapsed seconds since a fixed point in time, the Unix Epoch which occurred 1970-01-01 00:00:00 UTC.
Unix is not unique in using a reference Epoch, they have been used in calender systems worldwide since ancient times.
We can obtain current timestamp on Linux via command line with date command:
stevee@ideapad-530S:~$ date +%s 1620155520
A timestamp as a time source can be used with any timer definition, whether point in time or recurring. It has advantage (compared to using numeric representations of individual time elements) that a single long number can be used for computation and conversion and we don’t need to worry about problems like variable number of days in month or leap years.
Timestamps and time and date conversion tricks
For a timer defining specific days of week, the first question might be how to obtain weekday from a unix timestamp (elapsed seconds since epoch)?
int weekday = (floor((ts / 86400)) + 4) % 7;
1970-01-01 was a Thursday, dividing timestamp by 86400 (number of seconds in a day: 24 * 60 * 60) gives number of days since epoch, adding 4 shifts start day to Sun and modulo 7 returns day of week.
To check if a timestamp is within range of one or more on/off time pairs (specified in hh:mm format as uint8_t Min; uint8_t Hour;) first we convert all time elements to elapsed seconds:
// convert fully qualified timestamp to elapsed secs from previous midnight
unsigned long elapsedTime = ts % SECS_PER_DAY;
unsigned long s1, s2, onTime, offTime;
// check each timeArray on/off pair
for (int i = 0; i < _timeArray->n; i++)
{
s1 = _timeArray->onTime[i].Min * SECS_PER_MIN;
s2 = _timeArray->onTime[i].Hour * SECS_PER_HOUR;
onTime = s1 + s2;
s1 = _timeArray->offTime[i].Min * SECS_PER_MIN;
s2 = _timeArray->offTime[i].Hour * SECS_PER_HOUR;
offTime = s1 + s2;
if (elapsedTime >= onTime && elapsedTime <= offTime)
{
return true;
}
}
Conclusion
While TimedDevice library is non-blocking (it does not technique like delay()) it is not truely asynchronous or event driven as each device implementing a timer must poll for an event on each iteration of loop().
This could constrained to checking once per second/minute/hour but perhaps a better architecture would be to use either RTC DS3231 squarewave or Arduino internal timer to register and trigger an interrupt with an associated handler only when an event is due to occur.
Similarly if either a very large number of events are scheduled, or a large set of timed devices created, it would be sensible to register these with a scheduler (akin to a CPU scheduler) tasked with sorting, prioritising and actioning event queue in an efficient way, which might utilise a multi-threaded approach on multi-core CPU architectures.
Source code for Timed Device library can be found on GitHub including a full Arduino sketch example for defining a solenoid valve timer with an RTC timesource.